|
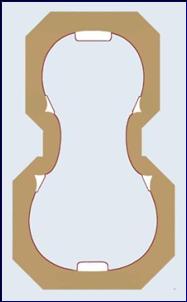
Violin mode A0 and A1 |
|
First cavity mode (Air zero). Depends on the volume of air within the body and on the area of the
Nodale line of A0 cavity mode
Mode A0 without a sound post Mode A0 with a sound post
The A0 cavity line nodal region will be activated on the back plate without a sound post to avoid any confusion with the nodal line of the top plate’s coupling frequency. Their frequencies are close or identical. Likewise true when using software.
On recent instruments, the A0 cavity frequency “without a sound post” must not exceed 246 Hz at 4,5% moisture content (Stradivari form). When the ribs must be lowered in order to raise the A0 cavity frequency, this must be done before gluing the neck: otherwise the back plate would have to be removed, which is not an easy matter.
Setting the neck and gluing the fingerboard do not modify the A0 cavity frequency “with or without a sound post.” The materials’ moisture content can alter it.
On a good violin, the cavity volume is between 1920 and 2020 cm3. This volume allows the A0 cavity mode frequency “without a sound post” to be tuned between 240 Hz and 246 Hz (270 à 286 Hz with a sound post) for f-holes totalling an aperture area of 8.5 cm2 to 9.5 cm2. Small apertures increase the air pressure and focus the harmonics as they exit the f-holes, thus increasing the carrying power of the instrument.
A frequency above 290 Hz produces several undesirable results: too clear and aggressive a timbre, with harsh dry low notes lacking consistency, a sour E-string, and saturated strings. Below 261 Hz, the sound tends to be cavernous and the timbre resembles that of a viola.
Adjusting the height of the ribs offers the possibility of modifying the interior volume of the violin body and consequently modifying the A0 cavity mode frequency. Increasing the rib height by 2 mm increases the cavity volume by approximately 100 cm3, thus lowering the A0 cavity mode frequency by 6 Hz. The opposite action will raise the A0 by 6 Hz.
If you do not wish to deviate from the standard rib height (30/32 mm), then, instead, you must change:
¨ -The area (cm2) of the f-hole apertures, ¨ -Or the flat area (cm2) of the violin model, ¨ -Or the height of the arching (more complicated), in order to obtain an appropriate A0 cavity mode frequency when necessary (depending on the model being copied).
If, in order to obtain a proper A0 mode frequency, the total area of the f-holes is greater than 10 cm2, harmonics will disperse as they exit, thus lowering the top plate’s mode 5 once the f-holes have been cut by as many as 75 Hz. This drop in frequency must be compensated by a heftier bass bar (heavier than 5 g) in order to raise the mode 5 frequency of the top plate with bass bar to an appropriate level.
N.B. The software (Patrick Kreit©) to calculate the A0 cavity mode frequency “without a sound post” supplied on the CD with the book yields more.
Violin mode A1
La fréquence du mode A1 se cacule en multipliant la fréquence du mode A0 sans âme par 1,9, ou en mulitipliant la fréquence du mode A0 avec une âme par 1,69.
Cavity volume on old violins
Cavity volume varies considerably among known Italian violins: 1780 cm3 to 2070 cm3. In general, violins by Amati and by Stradivari (before 1705) have a large cavity volume because, on the one hand, the arching at that time was higher, and on the other hand, Stradivari constructed larger violin models (including the “long Strads”) than Amati.
Around 1705, after many years of research, Stradivari adopted a smaller standard violin model with lower arching. He optimized the cavity volume, f-hole aperture area, and A0 cavity mode frequency, and raised the frequencies of the free back and top plates. Around 1709, Stradivari attained perfection. The greatest solo violins were conceived thereafter.
The smallest cavity volumes are generally found in violins by Guarneri, who tuned the A0 cavity frequency “with a sound post” between 280 and 290 Hz and thus, higher than Stradivari’s violins which average 272 Hz. Guarneri also built some violins with cavity volume equivalent to that of Stradivari’s instruments, but with a greater f-hole aperture area in order to raise the A0 cavity mode frequency.
The cavity volume for a modern violin must be between 1940 cm3 and 2000 cm3 at 6% moisture content in the wood of the sounding box in the white (the average for fine Italian violins). For 12% moisture content in the wood of the sounding box, add approximately 50 cm3 to the above figures.
To obtain minimal weight in the free materials, the starting volumes of the back and top plates must be optimized, thus reducing the volume of wood excavated from the intrados and hence, decreasing the cavity volume.
To obtain minimal weight in the free materials, the starting volumes of the back and top plates must be optimized, thus reducing the volume of wood excavated from the intrados and hence, decreasing the cavity volume. Decreasing the cavity volume increases the A0 mode frequency. Therefore, the area of the f-hole apertures must be reduced in order to obtain an average A0 mode frequency of 242 Hz “without a sound post.” Smaller f-holes result in a smaller decrease in the “initial” frequency of the top plate once they have been cut.
The top plate is stronger, thus enabling the maker to optimize the bass bar in order to raise the frequency of the top plate “with f-holes” back up to its “initial” frequency. Smaller f-holes concentrate the harmonics more as they exit the sounding box with increased air pressure, thus increasing the carrying power of the violin.
Optimizing the following characteristics –low arching, top and back plate weight, bass bar weight, strength of the materials, restricted f-hole apertures– contributes to the performances of the violin.
Large openings decrease the air pressure at the exit of the f-holes, whereas this pressure is already relatively low in the sounding box of a violin.
When the cavity volume is too great, or too small, the height of the ribs must be reduced or increased.
Violin model
Differences in the shape of the C-bouts or the upper or lower curves are not fundamentally important: what matters is to contain the volume of air of the body by optimizing the perimeter of the violin, in order to obtain a suitable cavity frequency by restricting the area of the f-hole apertures. It should be noted that, due to their higher A0 and A1 cavity frequencies, Guarneri’s violins have a clearer timbre than Stradivari’s.
The violin as we know it today is the result of one hundred fifty years of research, culminating in the “golden period” of Stradivari. It does not need to be re-invented, only rediscovered. This is why it is always preferable to make a copy, but not of just any violin. The choice should be focused on the finest Italian instruments, or in any case, a model that meets precise acoustic norms. Stradivari and Guarneri brought the violin to the height of perfection, so a personal model should not depart from known references, as any deviation would require new research to perfect the instrument.
When building their instruments, the Italian violin makers used a simple and reproducible technique, consisting in shaping the starting volume of the extrados (exterior) of the top and back plates by seeking their respective notes, before carving out the intrados (interior). Plate tuning was accomplished by tapping, then comparing the note heard with any instrument producing sound. Embedding the purfling, scraping, and finishing the edges were executed on the top and back plates glued separately onto the ribs. Thickness graduation in the purfling channel, in the center, or in the intermediary regions enabled the violin makers to tune the frequency of the top and back plates to a specific frequency, according to the desired timbre and robustness of sound.
This tried and tested technique was known even before Stradivari’s “golden age.” However, lengthy training must have been necessary before achieving accurate tuning of the materials by this empirical method. Due to the recurrent hygroscopic instability of the wood, particularly in an unheated workshop, this technique yielded a variable rate of success and was difficult to pass on. In his treatise, Félix Savart pointed out the problems in violin plate tuning entailed by moisture in the wood. Legend has it that the Italian violin makers fashioned their instruments during the winter and varnished them in the summer. All legends are based on an element of truth.
The difference between antique and modern violins must be sought in the development of a forgotten methodology. For a myth to persist, there must be an element of truth. Even during his lifetime, Stradivari was the world’s most famous violin maker. The greatest center for violin making during the 17th and 18th centuries was Cremona, where kings and their courts ordered their instruments, and each workshop had its own techniques, handed down verbally from father to son or from master to student.
The difficulty in research on former violin making techniques has always been to acknowledge and understand the difference between the old masters’ technology and that available to us today. What do we know about Italian violins? That they have an extraordinary sound! We are seeking that which has already been found, while remaining unaware of the method: that is the veritable secret! Over the course of two centuries, many explanations and hypotheses have been proposed, including a forever-lost recipe for a varnish with wondrous properties. In fact, it is simply a matter of understanding the laws of acoustics applicable to the violin, as well as the laws of physics concerning the materials constituting the instrument.
The art of violin making is so complex that it melds with science. Certain processes obtained through structured knowledge, close observation and objective experimentation (empiricism) can be considered as belonging to the realm of science.
Once they have been mastered, they remain simple workshop techniques perfected by highly trained craftsmen. This simplicity enabled the Italians to construct their finest violins without the help of our modern technological methods (albeit with a variable rate of success, due to variations in the moisture content of their materials). After a change in the practice or the disappearance of a craft, these techniques become secrets.
An historic process has eluded us; our modern means prevent us from distinguishing between myth and reality, between science and art. With the passing of time, they came to be considered as magical; intense questioning and reasoning yielded to mystification.
In order to copy an old instrument and obtain the same frequencies, it is essential to know the moisture content in the wood corresponding to these frequencies. The plate frequencies of the finest violins by Stradivari and Guarneri have long been known: they all lie within a restricted frequency spectrum.
Rib garland
The use of either type of mold, inside or outside (the latter was used by Jean Baptiste Vuillaume around 1830), offers the same advantages and drawbacks, from the technical point of view. Like the top and back plates, the rib garland must have sufficient weight and strength. The thickness of the ribs will be adapted to the density of the materials used, in order to obtain a rib garland weighing from 58 g to 60 g. This weight depends on the material’s moisture content and density, on the height of the ribs, and on the violin model. For a rib garland weighing from 49 g to 65 g, the frequency ranges between 140 Hz and 250 Hz.
Silver linden (Tilia tomentosa) linings, spruce blocks and corner blocks constitute a good choice. The density of silver linden and willow is from 0.50 to 0.65 g/cm3; for spruce, from 0.35 to 0.52 g. Low-density materials are required for blocks, corner blocks and linings. Densities from 0.65 to 0.68 g/cm3 at 12% moisture content are suitable for the ribs. Their thickness depends on the density and elasticity. Wood with homogeneous density must be used so as to limit discrepancies in thickness, strength, weight, and frequency of the rib garland.
The height of the ribs does not modify the frequency of modes C2, B1-, and B1+, but it does affect modes A0 and A1.
Average rib height at the upper block: 30 mm Average rib height at the lower block: 32 mm
A rib garland can absorb as much as 2 g of water when moisture content in the materials rises from 6% up to 12%, thus provoking a decrease in frequency for the plates’ coupling frequencies and for modes B1-, and B1+.
Neck
The density of the wood used to make the neck is important. It must not exceed 0.62 g/cm3 for 6% moisture content in the wood, or 0.66 g/cm3 at 12%. This will avoid having a neck that is too heavy, with repercussions on the C2 mode frequency and on the violin’s tone.
To obtain a sufficiently high frequency for the neck mounted on the sounding box, the wood must have high transverse celerity and elasticity. A discrepancy of 130 Hz may exist between different neck blanks having similar dimensions.
The frequency of a completed free neck is between 415 Hz and 545 Hz, depending on the performances of the wood and its moisture content at the time. It would be a mistake to modify the scroll, peg-box, or the thicknesses, in an effort to modify the frequency of a free or set neck: only the choice of wood allows mastery of this frequency.
Warning: Set the neck in only after prior dehydration of the free back plate or sounding box, so as to prevent an increase in the fingerboard projection from 27 mm to 29 mm when the violin is first exposed to UVs after set-up (in the white or varnished).
Before setting in the neck, prepare a fingerboard to give it the standard thickness and width, without hollowing the underside: 7 mm thick at the nut and 11 mm at the wider end. The fingerboard with the nut will be temporarily glued onto the free neck to adjust its fit. Then remove the fingerboard in order to align the neck with the centerline of the top plate for the neck set. Various techniques are possible for setting in the neck, at the choice of the violin maker.
The frequency of a completed free neck is between 415 Hz and 545 Hz, depending on the performances of the wood and its moisture content at the time. It would be a mistake to modify the scroll, peg-box, or the thicknesses, in an effort to modify the frequency of a free or set neck: only the choice of wood allows mastery of this frequency.
The neck must be very near completion before being glued for the following reasons:
· drilling the peg holes lowers the frequency of the free or set neck by approximately 10 Hz;
· reducing the neck thickness by 1 mm lowers the frequency of the free or set neck by approximately 20 Hz;
· adjusting the foot of the free neck to set it in raises its frequency by 40 to 60 Hz;
· finishing the foot of the neck and the heel on a set neck lowers its frequency.
The neck should be set in with a height of approximately 6 mm extending above the top plate with a slight tilt down the bass side (0.3 to 0.5 mm maximum).
This practice balances the pressure and the height of the strings on the bridge, as well the curve of the latter. This equilibrium also makes the instrument easier to play. The E-string thus elevated prevents the frog from striking the edge of the C-bout during bowing.
This tilt technique (poiriette) can be implemented on the fingerboard if modification of the neck angle is undesirable.
String Angle
In modern violin making, it is advisable to maintain the same angle of the strings 158°.
Depending on the height of the top plate arching, in order to obtain a constant string angle of 158° with a bridge 32 mm high (1.26 inches), the height of the neck above the top plate must be modified, as well as the height of the lower nut, if necessary, so as to keep the fingerboard nut aligned with the continuation of the rib line (± 1 mm).
The strings exert vertical pressure on the top plate, partially compensated by longitudinal compression that prevents the arch from collapsing towards the inside of the violin body. Vertical force is also exerted on the intrados of the back plate as it receives pressure from the top plate through the sound post.
Unlike the top plate, the back plate does not undergo longitudinal compression, but an elongation neutralizing expansion of the extrados tending to draw the back plate inwards. Under tension from the strings, the neck forms a force couple with the heel. Likewise, under tension from the strings, the tailpiece forms another force couple with the lower ribs. These two constraints tend to lengthen the back plate by balancing the opposing forces.
The resultant of the back’s elongation, tending to push the sound post upwards, must equal that
To achieve this equilibrium, the neck must be glued such that the nut lies on an imaginary line prolonging the line of the ribs under the edges of the top plate.
· The frequency of a set neck without a fingerboard and without pegs is between 220 Hz and 270 Hz, depending on the wood’s performances and moisture content (6% to 12%).
· A neck with low elasticity and celerity and too low a frequency gives the violin a dark timbre, even if the top plate’s coupling frequency is high.
· When this frequency is relatively low, the frequency and density of the unfinished fingerboard must be sufficiently high to offset the frequency.
· However, it is advisable for the frequency of the set neck to be no less than 245 Hz at 6% moisture content in the neck.
Copyright © 2010 - 2019 Patrick Kreit. Reproduction of any content of this site without my express written permission is prohibited
|